Tag Archives: TikZ

Oscar Flub

Could Typography have saved the Oscars?

Leave a reply

The 2017 Oscar ceremony brought a strange twist that could only have made Steve Harvey smile. The most anticipated award for Best Picture was first given to the movie, La La Land. After a several minutes long acceptance speech by La La Land's producers, the true winner of the night -- Moonlight -- was eventually announced. So the biggest question is: how did this happen and could it have been prevented?

The mistake has been attributed to two PwC accountants handing the wrong envelope to Warren Beatty and Faye Dunaway. During the presentation, Beatty clearly looks confused. Dunaway, thinking that her 1967 Bonnie and Clyde co-star was pausing for dramatic effect, makes the announcement for La La Land. Beatty explains when he read the card, he paused because it read Emma Stone. This could have been prevented provided certain redundancies were put in place. As embarrassing and painful as this must have been for everyone involved, we can always count on the internet to put its own hilarious take on things.

https://twitter.com/SethMacFarlane/status/836087279315648516

The Mistakes the Academy Made

The mistake the two PwC accountants made is understandable. So too is the mistake made by both Dunaway and Beatty. Given how hectic and stressful it must be to work behind the scenes while ensuring that everything runs smoothly, it is a surprise this has not happened more often. If anyone must be blamed, it should be the Academy of Motion Picture Arts and Sciences.

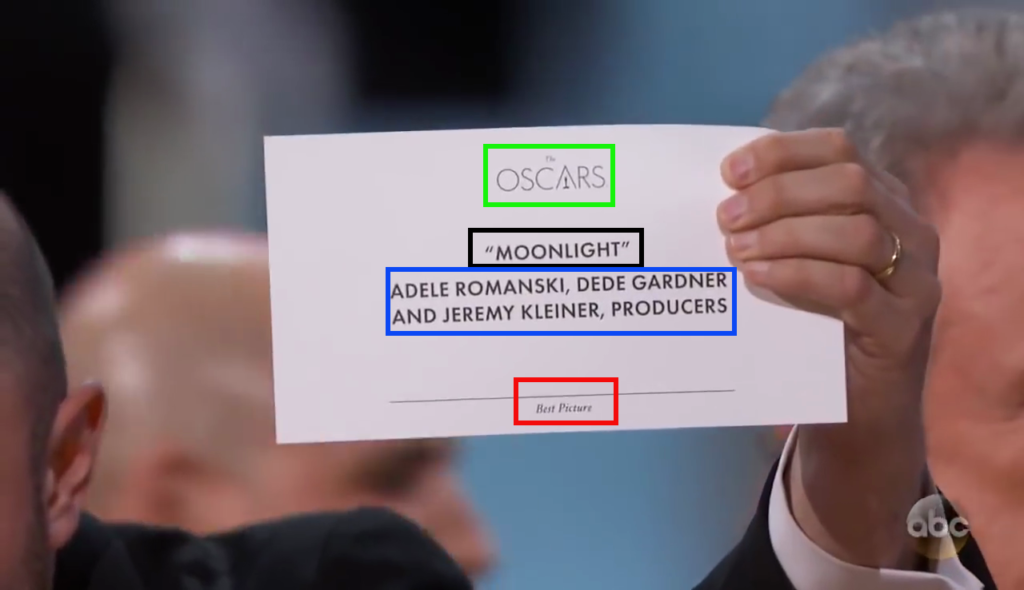
A screengrab from the ABC News YouTube video of the event shows the cue card. The design gives us some clues on why this mishap may have happened. The cue card for Best Picture has the movie title in the same font size, weight, and style as the film's list of producers. This makes distinguishing these two fields difficult at a glance. Good typography should make this effortless. The award being given is also not noticeable at first glance because the words Best Picture is written in small, italicized font at the bottom. In fact, most likely, you probably missed it. At least we know which awards ceremony we are watching as the words The Oscars is prominent on top.

typography oscar flub
Poor typography may have contributed to the Oscar flub (Credit: ABC News).

Solving the Oscars' Cue Card Problem

Before we can propose a good card design, we need to establish some goals for the card. The card should, at a glance, tell the reader or announcer:

  1. The prize being awarded (red).
  2. The person, or film receiving the award (black).
  3. the ceremony (green).
typography oscar flub


In the case of the award being given to a person, the cue card should show the film that person worked on while for a film, it should list the people involved as well as their roles.

Next we figure out the level of importance each piece of information represents. A person reading the cue card will usually scan the card, their eyes focused on the middle of the card. They will announce the person who won the prize, followed by the film they were in. If the award is going to a film, that gets announced followed by the people who worked on the movie. These two are the most important pieces of information on the cue card. Next in importance is the prize being awarded. We can assume that the announcer will be told this before appearing on stage so this information exists for verification purposes. If this piece of information was more prominent on the cue card, either Dunaway or Beatty could have caught it and notified the PwC accountants. As odd as it sounds, the least important piece of information is the award ceremony. We all know which ceremony we are attending and this placement exists purely for branding purposes.

By varying a font's style, width, position, and weight, we can draw a reader's eye to what is important and what is not. We need to make the field highlighted in black the most prominent, followed by blue, then green, and lastly red. We also need to place this information in the center of the card. Steve Harvey's 2016 Miss Universe flub was also the result of bad design - the 2nd and 1st Runner Ups were placed on the left side of the cue card while the winner was placed on the bottom right. This poor placement meant that Harvey's hand was blocking the pageant's winner.

TikZ Code for an Oscars' Cue Card

We can code this in the LaTeX graphics package, TikZ. We want to put the information that an announcer needs to read in the center of the card. This is where their eyes will focus as they pick up the cue card to look at it. We can change the font's weight and size to further highlight and draw an announcer's eyes to what is important.

Oscars Typography
We can place the information an announcer needs to read near the center of the cue card (black and blue).

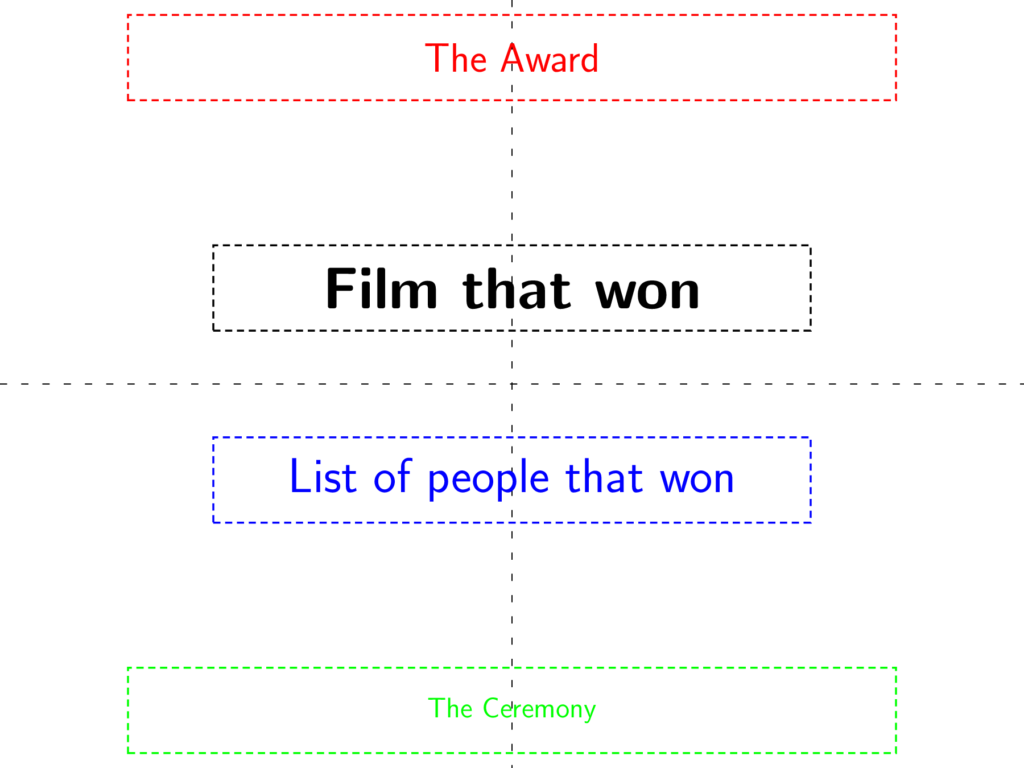
Our final card looks something like this. We are going to make the font for the person/film that won the largest and in bold. The font for the next piece of information will be smaller and not bold. The font for the award will be smaller still but still large enough that it can be seen and read easily. Last, the font for the ceremony will be the smallest size. The Academy will probably object to this but we aren't marketing a product where branding is important. We have an award ceremony to run.

Typography Oscars Layout
Where everything will go showing font size and weights.

Proposing a Layout

Now that we have established our goals and how they should be laid out, we can propose a card design. The font for the ceremony can be replaced by a logo and to add a little more emphasis for the award, we can put that in italics.

typogrpahy Oscars
A proposed cue card design for the Oscars

This should make things easier to read. The person announcing the award can tell, at a glance, the award they are supposed to read as well as who won that award. If they are not sure, the fact that they are announcing Best Picture can easily be seen above and the logo, while smaller, is noticeable to keep the Academy happy.

Going Further... Automation

We can go even further once we have everything in place. With LaTeX, we can create macros for each field and a new environment to contain it all. This will allow us to automate the process of creating cue cards.

Each new cuecard environment will typeset a new cuecard. There are packages that allow us to merge data from a CSV file in LaTeX, but we can also go for a fully automated solution, using something like Python or the R statistical language to query a database and generate the LaTeX code to typeset as many cuecards as you need. The LaTeX code can then be executed and the resulting cue cards printed.

Conclusion

We may not often think it but good typography matters. It makes reading effortless. It allows the reader to focus on what is needed and extract that information. The flub on Sunday night's ceremony was a result of poor typography and card design. A well-designed card means that either Dunaway or Beatty would have seen they were given the incorrect card and asked for a new one.

Fill Rules

Fill Rules in TikZ

Leave a reply

Filling shapes (or any path for that matter) in TikZ can be done with the \fill command. This requires very little thought on our part when it comes to filling simple shapes, e.g. circles or squares but it gets a little more complicated once we draw shapes with intersecting paths or holes. This is a difficult problem because we don't always know where the "inside" of a shape lies--this is not as simple as it sounds. To do this, we must understand the types of polygons there are as well as the rules for filling them with color.

Types of Polygons

We can divide polygons into two types: standard polygons and general polygons. Standard polygons are include circles, squares and triangles. These shapes have no holes and their paths don't self-intersect unlike general polygons.

Filling Shapes
The circle, square and triangle are basic polygons. Their paths do not intersect and the shape does not have a hole unlike the general polygon below.

Filling Shapes

There are two rules we can use to fill fhapes in TikZ:

  • Even-Odd Parity Rule
  • Non-zero Winding Rule

Both rules are algorithms that are used to determine whether a given point falls within an enclosed curve. To determine the "insideness" of a point, we draw a ray from the point we wish to determine to infinity in any direction. With the even-odd rule, we count the number of times the ray crosses a path segment. If the number is odd then the point lies on the inside of shape. If it is even then it lies on the outside.

Unlike the even-odd rule, the non-zero winding rule relies on knowing the stroke direction for each part the ray crosses. The number of intersections is scored and given a winding number. If the path is clockwise, or runs left to right, we subtract 1 from the score. If the path is counter-clockwise, or runs from right to left, we add one to the score. If the total winding number is zero then our point lies on the outside but if the winding number is not zero then the point lies on the inside. We will see how both rules differ and why.

Even-Odd Parity Rule

Fill Rules
We construct rays, both inside and outside, going through our shape of interest to determine if a point lies on the inside or ourside.

For a standard polygon, the shapes shown on top, it is easy to see where the outside lies but let's construct a few rays (shown in black) that lie outside and see what we get. For the circle, square, and triangle, the ray crosses the shape's path twice. This sum is even and we can conclude that the point lies on the outside of those shapes.

Now we construct some rays (shown in red) that lie on the inside. We see that they all cross the shape's path once. This makes the sum of path crossings odd and we conclude that the point lies on the inside of the shape.

But what happens with the general polygon below? We see that the black ray crosses the general polygon's path four times--an odd sum. This point lies on the outside of the shape. When we look at the red ray we see it crosses the shape's path once and we conclude that point lies on the inside.

Now let's look at the blue ray as it goes out from the hole. There is some doubt whether that point lies on the inside or outside of this shape but we can apply the even-odd rule. We see that the blue ray crosses the shape's path two times, an even number of times, which means the point lies on the outside of the shape and we don't color this area.

Fill Rules
Filling shapes with the Even-Odd Parity Rule

So we see how we can implement the even-odd rule in TikZ and how it works. But how exactly does the Non-Zero Winding Rule differ and will the results be the same? As you have probably guessed, the answer is no. After all, why have two different rules that do the exact same thing?

Non-Zero Winding Rule

Fill Rules
With the non-zero winding rule we need to consider the direction the path goes.

The non-zero winding rule is different from the even-odd rule in that we must consider the direction the path takes as the ray crosses it. We draw the direction of the winding path so we can determine whether a point lies on the inside or outside of a shape.

Fill Rules
We use our rays to determine whether a point lies on the inside or outside of a shape.

We do the same thing with the Even-Odd Parity Rule with one exception--if the path runs counter-clockwise as we cross it, we add one and subtract one if it runs clockwise.

For the circle, the first path crossing runs from left-to-right so we subtract one. As we continue our ray, the next crossing runs from right-to-left and we add one. The sum of our path crossings is zero and we conclude, like in the case of the even-odd rule, the point lies on the outside.

We see that for the circle, square, and triangle, the results are the same for the even-odd rule. Things are a little different for the general shape seen below. While the red and black rays yield the same result, the blue ray gives us something very different. The first crossing of the blue ray goes from left-to-right, we subtract one. The next crossing also goes from left-to-right, we again subtract one. The sum of our crossings is -2. The point lies on the inside and we fill the "hole" with color.

Fill Rules
We see the different effect of the Non-Zero Winding Rule on general polygons.

Path Matters

Fill Rules
In the case of general polygons, the even-odd parity rule (shown left) gives a different result from the non-zero winding rule (shown right).

We see the even-odd parity rule and the non-zero winding rule give different results for general polygons. This doesn't mean this is always the case. Path direction in the non-zero winding rule is the determining factor for the results we get.

We can create a general polygon with a hole where one shape lies inside the other and where their paths do not intersect. We can use TikZ code to specify the path directions of the innermost and outermost shapes. On the left, the outermost square's path curves around in a clockwise direction but its innermost square curls in a counterclockwise direction. We see with the general polygon on the right, both the inner and outer squares both curl clockwise.

Fill Rules
We can construct a general polygon with non-continuous paths. The difference is that the left inner square's path is counter-clockwise while the one on the right rotates in the clockwise direction.

We know that the even-odd rule will leave the hole unfilled in both cases as we are just counting path crossings but if we were to use the non-zero rule, on both shapes? We see that the outcome depends on path direction. The shape on the left with a counter-clockwise inner square produces the same result as the even-odd rule but the hole is filled when the inner path goes in a clockwise direction.

Fill Rules
The non-zero winding rule can produce different results for the same shape. This is due to the path differences of the inner rectangle.

Conclusion

Filling shapes with color doesn't have to be a complex operation if you understand the two fill rules and how they work. Generally, the even-odd parity rule won't fill a hole but whether the non-zero winding rule does depends on the path direction of the hole. Once we understand that, drawing and coloring shapes in TikZ becomes very easy.